En la actualidad debido a la coyuntura post pandemia y crisis económica, las organizaciones buscan mejorar su productividad con la mejora de sus procesos. 

En ese sentido las organizaciones que han implementado la mejora continua como parte de su estrategia y/o filosofía de productividad, utilizan una serie de herramientas básicas que les permiten medir el éxito o desviaciones de todos aquellos procesos que se deciden implementar o modificar.

Aqui te mostramos las 7 herramientas:

1. ANALISIS DE PARETO

El diagrama de Pareto puede ser de gran utilidad para la toma de decisiones en una organización, ya que permite evaluar el nivel de prioridad de las acciones que debes tomar para llegar a los resultados que esperas.

Permite observar la importancia relativa de determinados fenómenos (defectos, fracasos, gastos, accidentes) o causas (experiencia del operario, clase de materia prima, modelos de máquina, condiciones operacionales), a partir de los cuales pueden establecerse prioridades.

USOS:

• Identificar un producto, bien o servicio, para el análisis de su mejoramiento de calidad.
• Identificar oportunidades de mejoramiento.
• Analizar las diferentes agrupaciones de datos, por ejemplo, tipo de producto, segmento del mercado, área geográfica, etcétera.
• Buscar las principales causas de los problemas y establecer la prioridad de las soluciones.
• Evaluar los resultados de los cambios efectuados a un proceso (antes y después).
• Cuando los datos pueden clasificarse en categorías y el rango de cada categoría es importante.

Pasos para su implementación:

• Decidir cuáles problemas desean investigarse; por ejemplo: objetos defectuosos, pérdidas en términos monetarios, ocurrencia de accidentes, etcétera.
• Decidir cuáles datos van a necesitarse y cómo clasificarlos; por ejemplo: por tipo de defecto, localización, proceso, máquina, trabajador, método.
• Resumir los aspectos que se presentan con poca frecuencia en la categoría de “otros”.
• Definir el método de recolección de datos y el periodo de duración de la recolección. Es aconsejable usar una hoja de verificación.
• Diseñar una tabla para conteo de datos, con espacio suficiente para registrar totales.
• Elaborar la tabla de datos para el diagrama de Pareto con la lista de aspectos, los totales individuales, los totales acumulados, la composición porcentual y los porcentajes acumulados. Organizar los aspectos por orden de cantidad y llenar la tabla de datos.

Un ejemplo de aplicación: Lista de problemas de una linea de producción:

2. GRÁFICAS DE CONTROL ESTADÍSTICO.

Es una herramienta que nos permite vigilar si un proceso se comporta de la misma manera a través del tiempo, es decir, si el proceso es estable; en caso de no serlo, es necesario identificar las fuentes que están originando la desviación, para eliminarles y/o reducirlas. 

La gráfica de control es como una película, es decir, es una sucesión de fotografías del proceso a través del tiempo, las gráficas de control se pueden usar con dos fines:

1) Para el análisis, se utiliza para investigar si el proceso está en estado estable.

2) Para controlar el proceso, se usa para mantener estable el proceso.

Según el tipo de gráfica son:

1. Gráficos de control datos continuos

1.1 Gráficos de control x-r

Son gráficas de control basadas en datos continuos sus características son:

Son usados para variables continuas (por ejemplo un diámetro expresado en cm) y tenemos la posibilidad de sacar una muestra que puede ir de 2 a 9 piezas, hay que considerar que los datos deben ser normales e independientes además de seleccionar subgrupos o muestras racionales que permitan excluir causas especiales dentro de cada subgrupo.

Si un punto cae fuera de los límites de control es posible que el proceso ya no sea estable, e igual sucede en el caso de la gráfica R (rangos) que es la que monitorea la estabilidad de la variabilidad del proceso. 

1.2 Gráficos de control x-s

Es básicamente lo mismo que la gráfica x-r solo que en lugar de graficar el rango de cada subgrupo lo que se grafica es la desviación estándar del subgrupo.

La gráfica x-r es más común por su sencillez en los cálculos, pero ahora con los paquetes computacionales es más sencillo elaborar un gráfico x-s, sin embargo hay que notar que las mismas alarmas dará una y la otra, esto es no hay diferencia entre ellas en lo que respecta a su utilidad y depende los deseos de cada analista cual se adapta más a sus necesidades. 

1.3 Gráficos de medianas y rangos

Es una variante de los gráficos x-r,  solo que en este caso los promedios de los subgrupos no pueden ser calculados en forma conveniente o resulta más fácil para el usuario calcular la mediana,  de este modo utilizar esta gráfica para monitorear el proceso es más atractivo desde el punto de vista del usuario.

Las alarmas que arroja el gráfico y la efectividad de la misma para monitorear la estabilidad del proceso es como ya se dijo similar a la x-r.

Descargue un ejemplo de una gráfica Mediana – Rango  en excel

1.4 Gráficos de control individuales

Gráficas de Lecturas Individuales y Rangos Móviles (I,MR) para datos continuos individuales;  es un gráfico que es utilizado cuando no tenemos la oportunidad de sacar una muestra de tamaño n de la población en el tiempo t. El proceso solo nos permite tener un solo dato en el tiempo t.

Ejemplos de esta situación son procesos homogéneos por naturaleza como en los procesos continuos de elaboración de materias primas, ejemplo la fabricación de cemento, aluminio, pintura entre otros. 

Ya que tenemos un solo dato en el tiempo (I), nos podremos ver perjudicados por la distribución de la población de la que provienen nuestros datos, la cual podría no ser normal, cosa que evitamos en las gráficas x-r en las cuales podíamos tener un grupo de tamaño n el cual nos permite hacer uso del teorema de límite central y con eso conseguir la normalidad de la distribución de los datos.

2. Gráficas de Control para datos discretos o por Atributos

Muchas características de calidad no pueden representarse convenientemente de forma numérica. En estos casos, solemos clasificar cada artículo inspeccionado como producto conforme o producto no conforme con respecto a las especificaciones de calidad.

Los gráficos de atributos no suelen ser tan informativos como los gráficos de variables continuas  porque normalmente hay más información en una medición numérica que en la mera clasificación de una unidad como conforme o no conforme. 

Sin embargo, los gráficos de atributos tienen aplicaciones importantes. Son especialmente útiles en las industrias de servicios y en los esfuerzos de mejora de la calidad no relacionados con la fabricación porque muchas de las características de calidad que se encuentran en estos entornos no se pueden medir fácilmente en una escala numérica.

2.1 Gráficos de control, p

Los gráficos P o de fracción de no conformidades se definen como la relación entre el número de artículos no conformes en una población con respecto al número total de artículos de esa población. 

Los artículos pueden tener varias características de calidad que son examinadas simultáneamente por el inspector,  si el artículo no es conforme o no se ajusta a la especificación de calidad en una o más características, se clasifica como no conforme.

Normalmente expresamos la fracción de no conformidad con un decimal, aunque en ocasiones se utiliza el porcentaje de no conformidad que es simplemente el porcentaje de la fracción no conforme.

Los principios estadísticos en los que se basa el gráfico p o de control de la fracción de no conformidad están basados en la distribución binomial y requerimos cumplir con el principio de independencia (cada unidad producida es independiente de las las unidades que se produjeron en el pasado), y que la muestra se tome sea de manera aleatoria.

Si se selecciona una muestra aleatoria de n unidades de producto, y si D es el número de unidades de producto que no son conformes, entonces D tiene una distribución binomial con parámetros n y p.

La fracción de no conformidad será: 

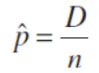
2.2 Gráficos de control, np

Es posible diseñar un gráfico de control basado en el número de productos no conformes en lugar de la fracción de no conformes. Esto suele denominarse gráfico de control del número de no conformes (np). 

Muchas personas que no tienen una formación en estadística encuentran el gráfico np más fácil de interpretar que la fracción no conformidades p.

En este gráfico se calculan los límites de control superior e inferior para que nos den un número entero de no conformidades, así el operador sabrá que si tiene más no conformidades que el límite superior que está dado en unidades el proceso está fuera de control al igual que si el número de no conformidades se encuentra por debajo del límite de control inferior el proceso estará fuera de control.

Se requiere un tamaño de subgrupo constante (n)  y dado que los Límites de Control se basan en una aproximación a la normal, el tamaño de muestra usado debiera ser tal que la  np ≥ 5.

Nota: En algunos procesos productivos se generan diferentes tamaños de lote en cada uno de los períodos de producción,  esta situación nos lleva a que el gráfico de control tenga un tamaño de muestra variable. Hay tres enfoques para construir y operar un gráfico de control con un tamaño de muestra variable sin embargo eso no lo tocaremos en este artículo.

2.3 Gráficos de control, c

Un artículo no conforme es una unidad de producto que no satisface una o más de las especificaciones para ese producto. Cada punto específico en el que no se satisface una especificación da lugar a un defecto o no conformidad. Por consiguiente, un artículo no conforme contendrá al menos una no conformidad.

Sin embargo, dependiendo de su naturaleza y gravedad, es muy posible que una unidad contenga varias no conformidades y no se clasifique como no conformidad. 

Como ejemplo, supongamos que estamos fabricando computadoras personales y  cada unidad podría tener uno o varios defectos muy pequeños en el acabado de la carcasa, y dado que estos defectos no afectan gravemente al funcionamiento de la unidad, la unidad se podrían clasificarse como conforme, pero si hay demasiados de estos defectos, la computadora personal se debra clasificar como producto no conforme, ya que tal cantidad de defectos serían muy perceptibles para el cliente y podrían afectar a la venta de la unidad

Hay muchas situaciones prácticas en las que se prefiere trabajar directamente con el número de defectos o no conformidades en lugar de la fracción no conforme.

Por ejemplo, el número de soldaduras defectuosas en 100 m de oleoducto, el número de remaches rotos en el ala de un avión, el número de defectos funcionales en un dispositivo lógico electrónico, el número de errores en un documento, el número de clientes que deciden abandonar un sistema de servicio sin completar su solicitud de servicio, etc.

Es posible desarrollar gráficos de control para el número total de no conformidades en una unidad o el número medio de no conformidades por unidad. Estos gráficos de control suelen suponer que la ocurrencia de no conformidades en muestras son de  tamaño constante son modeladas por la distribución de Poisson.

2.4 Gráficos de control, u

Ahora se puede dar el caso de que no sea factible un tamaño de muestra exactamente igual a una unidad de inspección. 

La unidad de inspección se elige para simplificar el funcionamiento o la recolección  de datos. Sin embargo, no hay ninguna razón por la que el tamaño de la muestra deba limitarse a una unidad de inspección. 

Así pues podríamos establecer un gráfico de control basado en la media o número de no conformidades por unidad de inspección. Si encontramos x no conformidades totales en una muestra de n unidades de inspección, el número medio de no conformidades por unidad de unidad de inspección es:

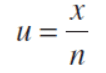
Obsérvese que x es una variable aleatoria de Poisson; en consecuencia, los parámetros del gráfico de control para el número medio de no conformidades por unidad son los siguientes

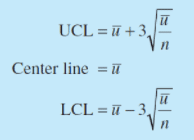
IMPLEMENTAR EL CONTROL ESTADÍSTICO DE PROCESOS:

Para la implementación de los gráficos de control o el control estadístico de procesos implica la aplicación de dos pasos.

En el paso I, se recopila los datos del proceso y se analizan, construyendo límites de control de prueba para determinar si el proceso ha estado bajo control durante este periodo de tiempo y con ello  ver si se pueden establecer límites de control fiables para supervisar futuros procesos.

Luego, comparamos los “n” puntos muestreados con los límites de control que son calculados a partir de esos mismos puntos

El objetivo es encontrar los puntos que se salen fuera de los limites de control e investigar las causas especiales que de ellas deriven para eliminarlas.

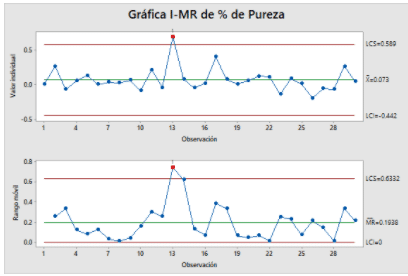
Una vez que se hayan resuelto las causas especiales debemos volver a correr el proceso y recolectar datos para hacer de nuevo el cálculo de los límites de control. 

Es importante también verificar que los supuestos de normalidad e independencia y la toma de muestras racionales sean tomados en cuenta. 

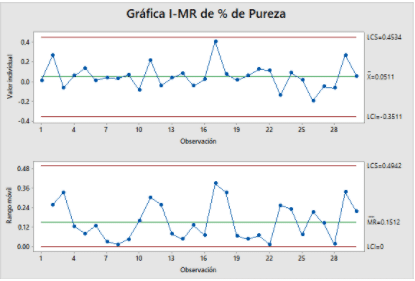
Finalmente, el proceso se estabiliza y se obtiene un conjunto de datos limpios que representan el rendimiento del proceso en control para su uso en el paso 2.

En el paso 2, el proceso se encuentra en estado estable y utilizamos el gráfico de control para controlar el proceso comparando los datos o muestras  con los límites de control, verificando así la estabilidad del proceso en curso.

Durante esta fase, el análisis de datos y la reacción a causas especiales se realiza en tiempo real,  una vez que el proceso es estable y predecible  podemos conocer su capacidad para cumplir de manera consistente con lo que el cliente desea.

3. ESTRATIFICACIÓN.

Estratificación consiste en clasificar los grupos de datos con características comunes con el fin de simplificar el análisis de datos para la mejora de procesos o la solución de problemas. Las características comunes son referidas a la información histórica de los datos desde su origen (por ejemplo, quién y con qué material, maquinaria y equipo se ha manufacturado y producido, etc.) y la situación de la cual se ha tomado.

Como se estratifica

Los datos se deben de tomar clasificados en categorías, para lo cual se deben aplicar los conocimientos y experiencia técnica de los procesos de producción y de los mismos productos.

Los tipos de estratificación que se usan normalmente en áreas de trabajo son los siguientes

• Por material y materia prima.
• Por proveedor, por lugar de origen, por marca, por fecha de compra, por lote de recibo, por lote de producción, por elementos, por tamaño, por partes, por tiempo de almacenaje, por lugar de almacenaje, por condiciones y fecha de producción, etc.
• Por equipos y maquinaria. Por tipo de máquinas, por cantidad de máquinas, por modelo de máquina, capacidad, antigüedad, planta, línea, ajuste de máquina y equipos, guías y herramientas que se utilizan.
• Por operadores Por individuos, edades, años de experiencia, sexo, grupo, turno, etc.
• Por método de operación o condiciones de operación. Por velocidad de línea, método de trabajo, condiciones de operación, condiciones de establecimiento y ajuste. (Número de revoluciones de máquina, presión, temperatura), por lugar de operación, por lote, por método de medición, etc.
• Por tiempo. En la mañana y en la tarde, día y noche, inmediatamente después del inicio de operación, inmediatamente antes de la terminación, etc.
• Ambiente, medio ambiente, clima. Temperatura ambiente, humedad, despejado, nublado, lluvia, hay viento o no, tiempo de lluvia, seco, cercanía o lejana disposición, iluminación, etc.
• Por medición o inspección Por probadores, por calculadores, por encargados de medición, por inspectores, etc.
• Por características especiales. Si es producto nuevo o existente, si es la primera pieza, por defectos, por lugar del producto, por empaque.

En la figura, se muestra el ejemplo de obtención de buenos resultados realizando la clasificación por categoría para el mejor aprovechamiento del pigmento “A” en una fábrica de teñido. Al elaborar la gráfica de concentración, se observó mucha variación (desde 50% hasta 150%).

Se graficaron juntos los datos del horno 1 y 2 y se identificó el Horno No 1 con una “X” y el Horno 2 con una “O”. Resulta que en el horno No.1 hay más puntos altos que el valor promedio, en cambio que en el horno No. 2, hay más puntos bajos del valor promedio. Por esta razón se elaboró la gráfica estratificando en horno No. 1 y No. 2 (Por categoría). El valor promedio del horno No. 1 es de 124% y en el horno No. 2 de 78%; hay mucha diferencia. También se observa que la variación en cada uno de los hornos es la mitad de la variación total, por lo tanto, se investigó la causa y se encontró que la clave de la diferencia radicaba en el aspa del agitador. Se modificó el aspa del horno No. 2 a la forma presentada por el aspa del horno No. 1 y como resultado, se mejoró la concentración en 25% y se redujo la variación.

4. HISTOGRAMAS.

Con el histograma iniciamos el recuento de las herramientas de mayor peso estadístico. Excelente para entender si una variable importante de un proceso está dentro de especificaciones, y para visualizar la forma de la distribución de los datos.

Es una gráfica de barras que muestra la frecuencia con la que han ocurrido o se han presentado una serie de datos o fenómenos, así como su distribución, esto se logra a través de agrupar los datos en intervalos definidos y evaluar cuantos datos están contenidos en dichos intervalos (frecuencia).

Expresando los datos en un Histograma de frecuencias se puede conocer y analizar:

1) El comportamiento global de los datos (Forma de distribución)

2) Cuál es su comportamiento promedio (Posición central)

3) La magnitud de la variación de los datos.

4) Su comportamiento con respecto a la norma o especificación (índice de capacidad del proceso y/o porcentaje de defectos)

Interpretación del histograma.

Como se mencionó al principio, a través del histograma de frecuencias analizaremos la variación que presenta un proceso o fenómeno determinado.

Para hacer una correcta interpretación de la variación del proceso necesitamos definir el polígono de frecuencias, el cual nos dará una mejor idea de la distribución de frecuencias del fenómeno que se está analizando.

El polígono de frecuencias.

Es una curva que se obtiene al unir con una línea continua los puntos medios o extremos superiores de cada barra consecutiva del Histograma de frecuencias.

5. DIAGRAMA DE CAUSA-EFECTO (ISHIKAWA)

Es una importante y completa herramienta, que permite identificar las causas y posibles soluciones de un problema específico. Esta herramienta fue creada, en 1953, por Kauro Ishikawa, profesor de la Universidad de Tokio. Ishikawa es uno de los precursores de la calidad en Japón.

El diagrama causa-efecto muestra la relación entre la característica o efecto de calidad y sus factores o causas.

Ayuda a identificar las posibles causas de un problema de forma ordenada y estructurada.

Se usa para:

• Identificar las posibles causas de un problema.
• Ordenar las posibles causas en categorías.
• Documentar de manera rápida las causas.

Procedimiento para la elaboración del diagrama Ishikawa.

• Describir el efecto, atributo o variable de la calidad que va a analizar.
• Escoger esa característica de la calidad y se escribe en el lado derecho de la hoja; a la izquierda de ésta debe ubicarse la columna vertebral del diagrama.
• Escribir las causas primarias, que se denominan “ramas principales”.
• Escribir las causas secundarias que salen de las ramas principales y las causas terciarias que salen de las “ramas” medianas.
• Determinar todas las causas posibles que pueden afectar la característica.
• Es recomendable realizar trabajos grupales de discusión abierta y fomentar la “tormenta” de ideas.
• Agrupar las causas por afinidad, ramas grandes, medianas y pequeñas.
• Elaborar el diagrama causa-efecto con los elementos que parecen tener un efecto significativo sobre la característica de calidad.
• Asignar la importancia a cada factor, se marcan aquellos que parecen tener un efecto significativo sobre la característica de calidad. Depende de la experiencia personal.
• Registrar cualquier información que pueda ser útil: título, nombre del producto, proceso, lista de participantes, etcétera

Para manufactura use las 5 Ms y 1 A:

• Material
• Máquina
• Mano de Obra
• Método
• Medición
• Ambiente

Para servicios use las 4 Ps:

• Procesos
• Políticas
• Personal
• Planta – tecnología

6. DIAGRAMAS DE DISPERSIÓN.

El diagrama de dispersión grafica pares de datos (x,y) en una cuadrícula de dos ejes para buscar relaciones entre ambas variables. Si existe relación, los puntos seguirán la forma de una recta o una curva.

Se usa cuando:

• Se quiere establecer si existe relación entre dos variables.
• Se sabe que existe relación entre dos variables y se quiere modelar esa relación.
• Se quiere formalizar una causa raíz mediante análisis estadístico.

EJEMPLO:

Una heladería le da seguimiento a sus ventas con respecto a la temperatura a medio día. El estudio se realiza por doce días consecutivos. Los datos son los siguientes:

La temperatura es la variable independiente que vamos a colocar en el eje x, y las ventas son la variable dependiente y van en el eje y. El diagrama de dispersión resultante es el siguiente:

7. HOJAS DE VERIFICACIÓN

Es un formato que sirve para registrar, analizar y procesar fácilmente los datos registrados en él. Las condiciones para aplicar eficientemente esta hoja son:

• Elaborar la hoja de verificación que esté de acuerdo con la finalidad de uso.
• Debe ser lo más sencilla posible.
• Los puntos de verificación deben ser estudiados constantemente.
• Reglamentar el método de verificación. 5. Los puntos de verificación deben coincidir con el orden de la operación.
• Aclarar la secuencia de datos.
• Tomar las medidas y contramedidas oportunamente.
• Debe de estar diseñada de tal manera que se puedan tomar con facilidad las acciones correctivas.

¿Cómo usar la hoja de verificación?

A grandes rasgos, se pueden clasificar en tres grupos principales:

• Investigación.
• Verificación.
• Registros.

1. Investigación. Se utilizan para analizar e investigar situaciones de preocupación especiales, permitiendo conocer el tipo de defectos, su distribución, localización y cantidad.
2. Verificación. Con el fin de controlar los trabajos diarios, se verifican ciertas actividades periódicamente. De ante mano se definen los puntos a revisar y se lleva a cabo la verificación de acuerdo a esta hoja.
3. Registro. Se toman los datos en forma tabular para la elaboración de los reportes, para tener información que nos permita visualizar la situación global de un proceso y para apreciar sus variaciones a largo plazo. Diferencias y aplicación entre la hoja de verificación y la lista de verificación.